Ancient War Tricks and Mathematics

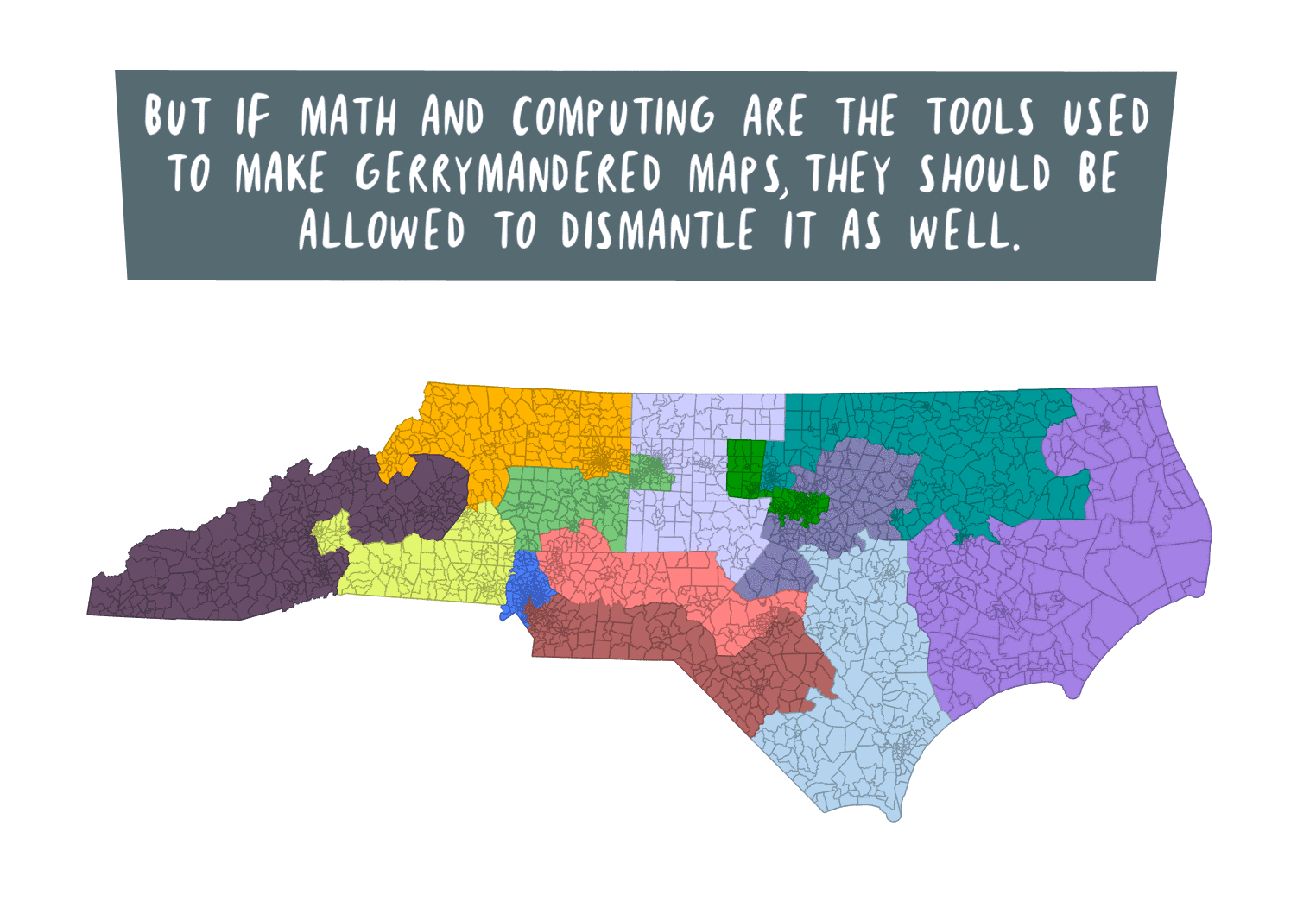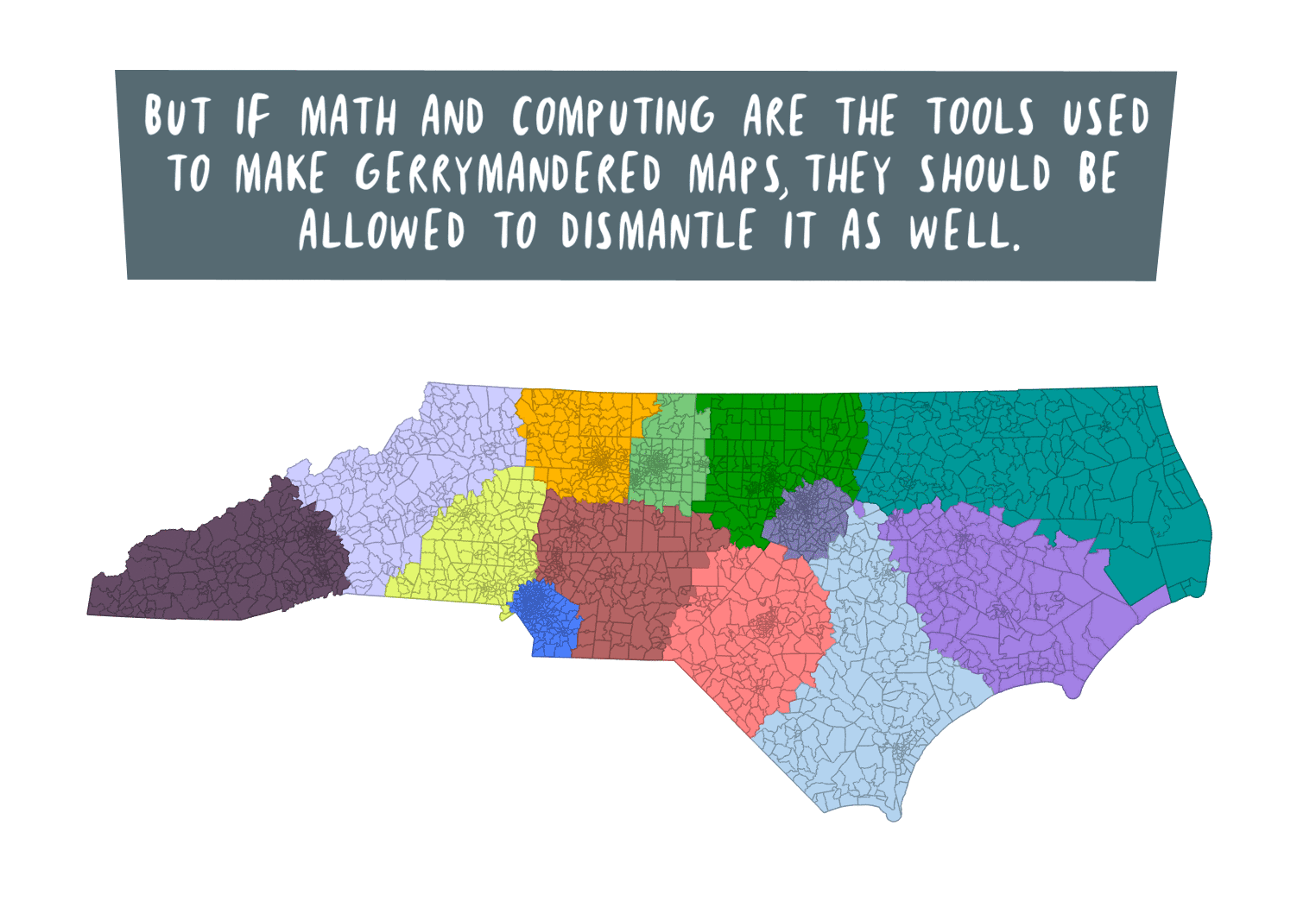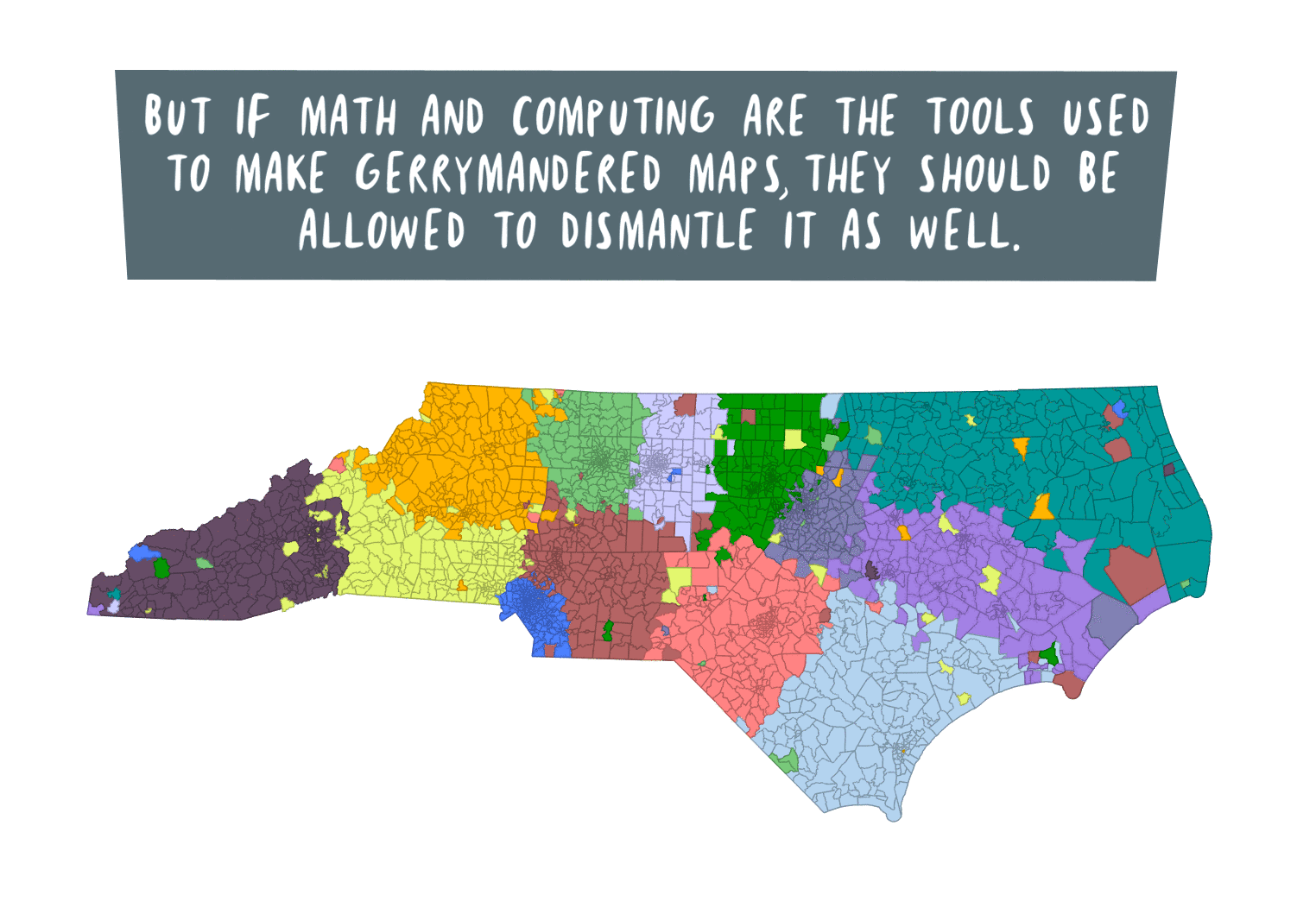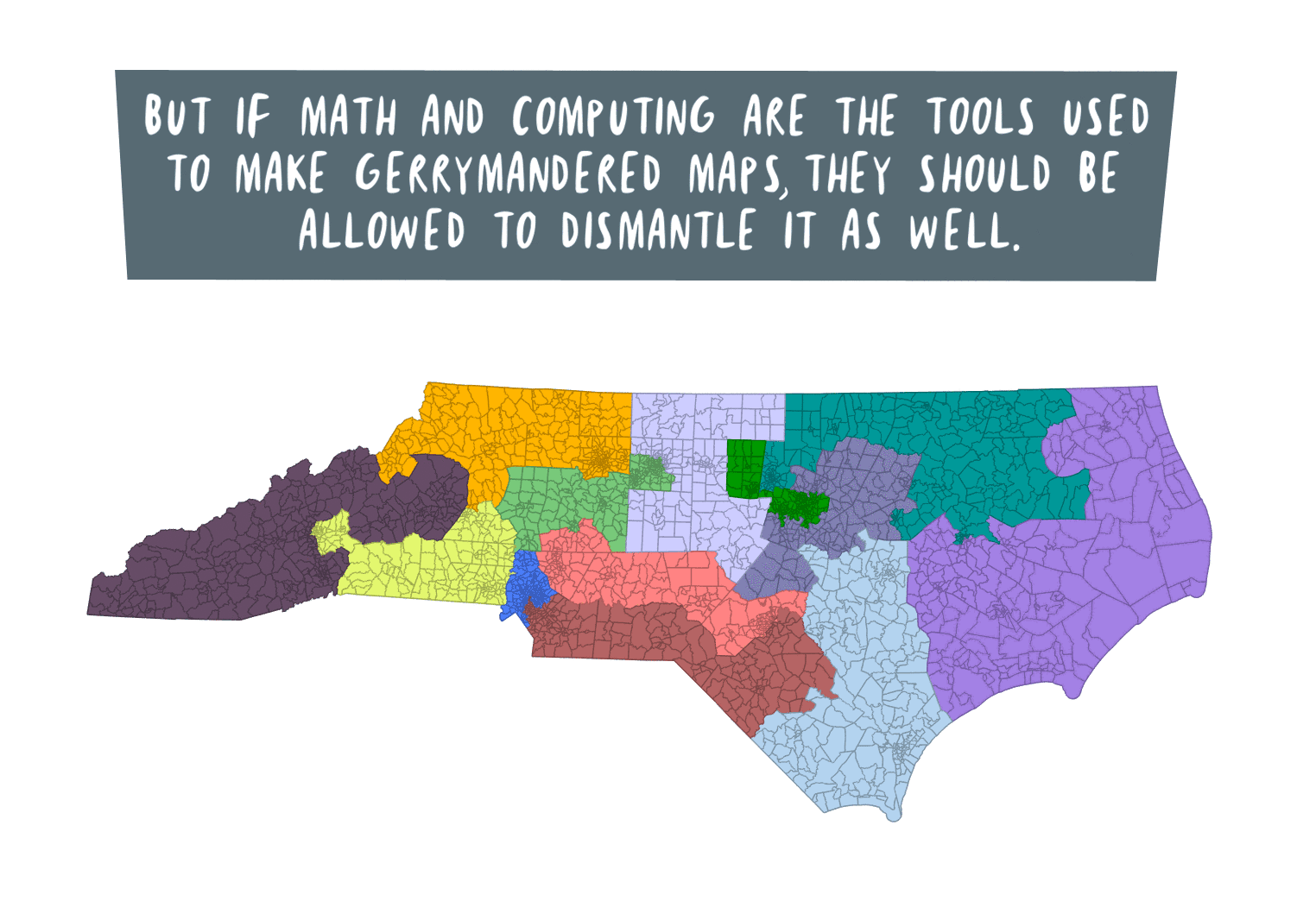
Quanta Magazine has an interesting article about how an ancient Chinese warfare technique is used in mathematics today, including making predictions for…comets? Check out the article here.

BADGING:

Read the article linked above.

Then, answer the following questions.

1. One of the first scenarios in the article states: “In a morning drill you ask your soldiers to line up in rows of five. You note that you end up with three soldiers in the last row.” Make a list of the first 10 possible number of soldiers that could fit this arrangement.
2. One of the next scenarios in the article states: “...then you have them re-form in rows of eight, which leaves seven in the last row.” Make a list of the first 10 possible number of soldiers that could fit this arrangement.
3. The third scenario in the article states: “…and then rows of nine (soldiers), which leaves two (soldiers in the last row).” Make a list of the first 10 possible number of soldiers that could fit this arrangement.
4. Explain how, once you found the first number shared by each of the three lists above, you could “jump ahead” to the next number shared by each of the three lists.
5. Define the term “pairwise coprime“. Give an example of two numbers that are pairwise coprime.

Why Does Voting Take So Long? Math and Racism.

There’s been a lot of attention paid to the amount of time it takes to vote in this 2020 Election recently. Turns out the main reasons are math and racism. WIRED can explain more.

BADGING:
Read the WIRED article linked above. Answer the following questions in a few sentences each.

1. There are a number of variables (reasons) that can explain why some polling places have a long wait time. List some of them here, and give an explanation for one of them.
2. There are a few variables (reasons) that researchers surprisingly discovered did NOT have any effect on the wait time or not. List them here, and for one of the reasons explain why it might be a surprising discovery.
3. How could a better understanding of societal racism lead to decreased wait times in some voting locations?
4. Visit THIS LINK (this was created by the mathematician mentioned in the WIRED article to help visualize wait times at polling locations). This year, Mr. Bezaire waited for exactly 1 hour to vote, between 2 and 3 pm in the afternoon. Play with the variables on this graph to come up with any scenario that makes this wait time possible. Explain the variables required to make this happen.

How NASA uses Origami

Did you know that the ancient Japanese art of paper folding (origami) is mathematical in nature?  Did you know that NASA actually uses origami when designing spacecrafts?  Watch the video above to learn more!

BADGING:

Watch the video above.  In a short paragraph, summarize how NASA uses origami when designing spacecrafts.  Then, visit THIS PAGE of origami instructions to create any flower of your choice (if you don’t have suitable origami paper, Mr. Bezaire has some you can borrow).  Include a picture of this origami creation in your Badge Google Doc.  Then, write a second paragraph that describes different mathematical properties/ideas/concepts that you saw and experienced while making your origami creation.

Women are better than men at free throws

The results of a 30-year study show that women NCAA basketball players shoot free throws more consistently than male NCAA basketball players.  See the findings here.

BADGING:

Before reading the article, make at least three hypotheses that you think might be the reason women tend to be “better” at free throws than men in the NCAA.

Then read the article linked above.

Below your hypotheses, write a paragraph explaining what the study found.  What appears to be the major factor in the women’s free throw consistency?  Compare this finding to your hypotheses.

Write a second paragraph stating another athletic comparison that you would like to see studied (for example, “Who makes free throws more consistently, left-handers or right-handers?”).  It doesn’t have to be a basketball comparison.  Explain why you think this comparison could be valuable to athletes and coaches.

Thanks to Bradley Warfield for suggesting this badge!

W.E.B. DuBois at the World’s Fair

W.E.B. DuBois, the first African American to earn a doctorate from Harvard University, attended the World’s Fair in 1900 in Paris with some amazingly beautiful graphs (“Data Visualizations”) that showed what life was like for black folks in America at the end of the 1800’s.  Read about them and see the striking images by clicking here.

BADGING:

Read the article linked above.

Pick any three of the graphs from below the article that DuBois displayed at the World’s Fair.  For each of the three graphs you choose, answer these questions:

1. What is the title of the graph?
2. What aesthetic or artistic choices (colors, layout, design, etc.) did DuBois make in creating this graph?
3. How did those choices from the previous question add to the visual appeal of the data?  Why is this graph more effective than just listing the data as a table or a list of numbers?

Then, write a single paragraph that summarizes what you learned about what life was like for African Americans in the USA at the end of the 1800s (especially in the South).  What was DuBois trying to show the world by bringing these graphs to the World Fair?

Thanks to Jason Kissel via Chris Nho for suggesting this badging opportunity!

The Mathematics of the Black Panther

As part of Chalkdust Magazine‘s celebration of Black Mathematician Month 2018, Dr. Nira Chamberlain discusses one of Shuri’s creations in Marvel’s Black Panther movie; T’challa’s suit, which supposedly disperses energy from impact blows and absorbs the shock to minimize damage.  Is this mathematically possible?  Read on to find out!

BADGING:

Read the article linked above.

In a paragraph, describe what would have to be true about a suit that disperses kinetic energy in the way that Black Panther’s suit does in the movie.  A suit like that hasn’t been invented yet, but a mathematical model has been made.  Describe in your own words what characteristics that suit would have in order to make the energy dispersal possible.

In a second paragraph, think of some movie tech that doesn’t yet exist (choose a favorite movie that contains some sci-fi or futuristic element to it).  If you were to make a theoretical model of that tech, what type of mathematical and scientific questions would you have to address before attempting to build a prototype?  For T’challa’s suit, mathematicians had to determine how to disperse the shock of impact.  What would have to be mathematically feasible for different movie tech?  Be sure to tell me what movie and what tech you’re discussing!

Mayan Mathematics

Certain schools on the Yucatan Peninsula in Mexico are teaching native students the mathematics that was done by their ancient ancestors in the Mayan civilization.  Check it out in the video above.

BADGING:

Watch the video and pay attention to how the Mayans write their numbers and conduct simple arithmetic.  Answer the following questions.

1.  How would you express the number 19 using the Mayan notation?
2. In the video, the news reporter shows how to do the arithmetic 16 + 7.  Replicate that arithmetic using drawings.
3. Now create a drawing/notation using the Mayan method to conduct the arithmetic 18 + 6.
4. Explain at least three reasons why it is important for these children to be taught this method of arithmetic alongside the “typical” methods (like the way you learned to do addition, for example).

 

Lindsey Vonn Wants To Race Against The Men. Should the Olympics Allow It?

With the 2018 Winter Olympics in full swing, 538 has published an analysis of Men’s vs. Women’s skiing statistics.  In the history of the Olympics, men and women have always raced separately and received separate medals.  American Olympian Lindsey Vonn wants to be able to race against the men.  What do the numbers say about this?

BADGING:

Read the article linked above.  Answer the following questions in a couple of sentences each.

1.  In what skiing event(s), if any, do men appear to be consistently faster?  In what skiing event(s), if any, do women appear to be consistently faster?  In what skiing event(s), if any, does there not appear to be any discernible difference between men’s and women’s speed?
2. What other factor(s) do we need to take into account about the men’s and women’s skiing events besides their average speed?
3. Using the data provided in the article, write a short paragraph making an argument either FOR or AGAINST women racing against men in alpine skiing events.  (There is no correct stance to take on this issue, but you must use the data to support your claim.  Don’t just state your opinion.)
4. Does Lindsey Vonn think she would win against the men?  What do you think is her motivation for wanting to race against the men?

Fairy Circles and the Mathematics of Nature

Mathematician Dr. Corina Tarnita studies the mathematics of nature and biology, including things called “fairy circles”.  Watch the video above and read more about her work here (via Quanta).

BADGING:

Watch the video and read her interview at the link above.  Answer the following questions in a couple of complete sentences each.

1.  Explain (from the video) her comparison of liking magic tricks to understanding how nature works.  What did she mean by this?
2. What are fairy circles, and how does mathematics play a role in how termites help to create them?
3. What does Dr. Tarnita hope that “patterns” and “symmetry” will help teach them about the ecosystem in the African savannah?

Gerrymandering

Gerrymandering is the term for when political borders (shapes of districts, etc.) are set so that one political party/group gains an advantage.  It’s widespread, but there are some cases in the court system now trying to address the issue — and mathematicians are helping.  From The Nib comes a comic the describes mathematicians’ roles when it comes to Gerrymandering.  Check it out!

BADGING:

Read the comic linked above.  Answer the following questions in a couple of sentences each.

1.  Using the cartoon of red/blue houses, explain how gerrymandering can take an evenly split vote between two parties and make it a “majority win” for one of the parties.
2. Courts have rules against districts in the past for racially-based gerrymandering.  But why have the court systems been mostly powerless to rule on partisan gerrymandering cases to this point?
3. Mathematicians are tackling the unresolved question of how “compact” districts can be and how to define that compact-ness.  What are two ways that “compact” can be defined mathematically?
4. In your own words, describe what is meant by “negative curvature”.  Why is this a red flag for districts?
5. How are mathematicians using “maps that could have been” as a way to frame the gerrymandering discussion?